Can Entropy-based Sampling Make LLMs Reason Better?
Entropix attempts to improve reasoning in models through being smarter at sampling, instead of via more training.
Early work by XJDR seems to show that it can significantly increase reasoning in small models. This is particularly exciting because it gives AI developers more tools to understand the states their model is in, and can be done for any open source model, it doesn’t require additional traning.
Why use Adaptive Sampling?
Sampling is the process of choosing which token from the distribution of possible tokens (the logits) that a LLM chooses.
The ideal case is that your distribution always looks like this:
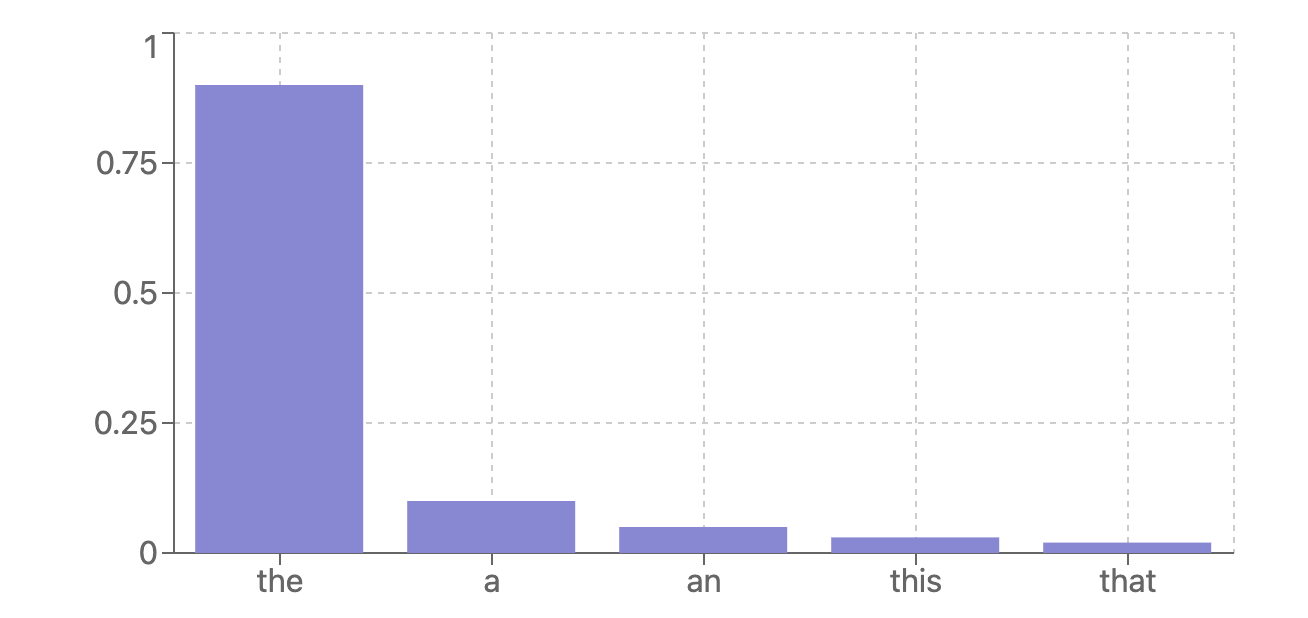
But in reality, models are never so sure of their predictions. You will often run into cases where the next token prediction looks like this:
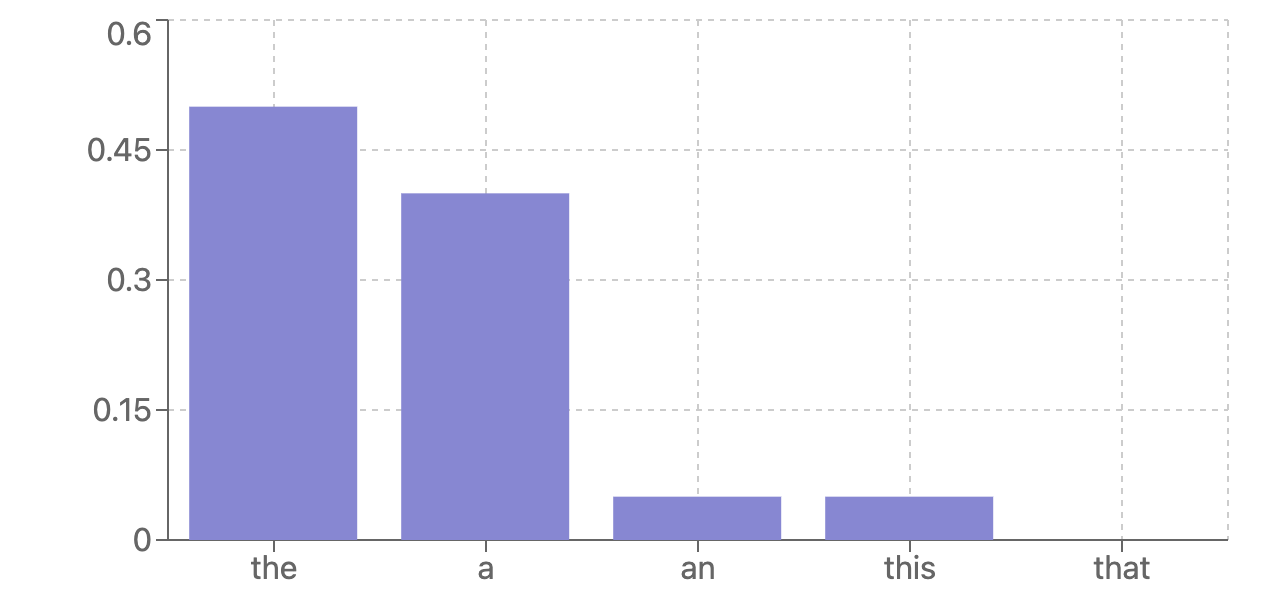
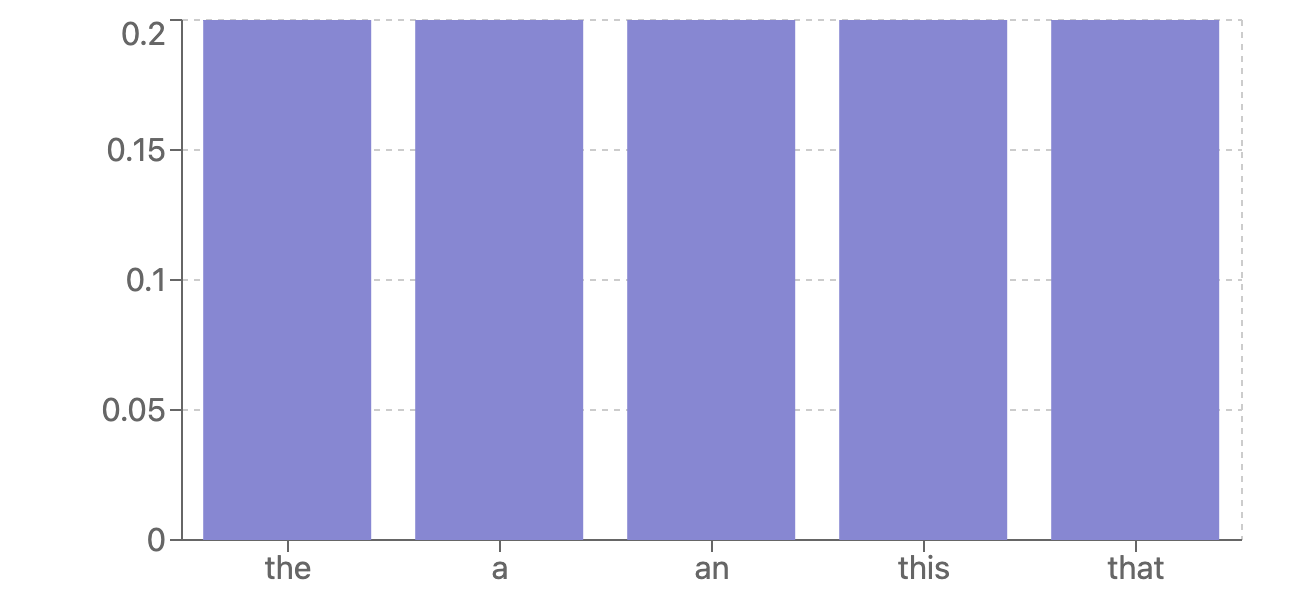
In these cases, the model is uncertain.
What does uncertainity mean, and does it matter?
Uncertainty might have many different underlying causes, for example:
- The tokens could be synonyms (e.g. good vs great)
- This could be the start of significant branching paths (e.g. the AI could either write your program in Java or C)
- The AI may genuinely not be sure what to do (it is ‘out of distribution’, it hasn’t seen this in its training data before).
Entropix suggests that you should have different methods for choosing the next token, depending on how uncertain you are.
How do we do that? To start, we need to measure uncertainty.
Entropy and Varentropy
The key tools that Entropix uses is measuring uncertainty via two metrics: the entropy & varentropy of the logits.
In this case, Entropy measures how different the predicted logits are from each other, i.e. how uncertain we are in the most probably outcome. In low entropy, we are pretty certain in a few of the logits. In high entropy, the distribution of the logits is more uniform and we are much less certain.
Varentropy represents the variance of the entropy across the different possible outcomes. It gives us an idea of the “shape” of the uncertainty. High varentropy indicates that some of the values are highly different from others.
Combined, the two of us give 4 possible states:
- Low entropy, low varentropy: A very peaked distribution (one highly probable outcome).
- Low entropy, high varentropy: A distribution with a few disparate peaks.
- High entropy, low varentropy: A uniform or near-uniform distribution.
- High entropy, high varentropy: A spread-out but uneven distribution.
Adaptive Sampling based on Entropy & Varentropy
Now that we have those metrics for uncertainty, we can develop strategies for how to use it.
Low Entropy, Low Varentropy
This is usually the ideal case. The model is certain not only in what its first option would be, but also what it would choose if the first option was incorrect. Often times this means that the list is ordered in a neat way.
In this case, adaptive sampling would suggest the standard argmax sampling, e.g. choose the token with the highest probabilitly.
Low Entropy, High Varentropy
In this case, the model predicts a few options very highly.
This is a tricky case- it may be representing a whole new branch of output, or it may be representing a few options such as a synonym.
In this case, we may want to “branch” by predicting both logits, seeing what paths they take and comparing the results. There are many ways to implement this branching, which we’ll discuss a little later.
Depending on the results of the branching, we might also want to ask the user. If we get two branches with fairly equal confidence (a measure of their entropy and varentropy) but different contents, we could formulate this as a question to the user.
High Entropy, Low Varentropy
This state represents a possible low confidence state in the model. It may be seeing something that it doesn’t recognize at all, or all the options may be interchangeable with each other.
The best thing to do here is to help the model get to a higher confidence state. The first step of that is reflection. We could insert a “thinking” token here as the next token, e.g. “Wait..” seems to be OpenAI’s thinking token.
This thinking token should ideally cause the model to generate reflection tokens until it gets to a high confidence space.
This could be an opportunity for new techniques like on-demand RAG, where you could train the model to consider function calling for more information when it realizes it needs to think more.
High Entropy, High Varentropy
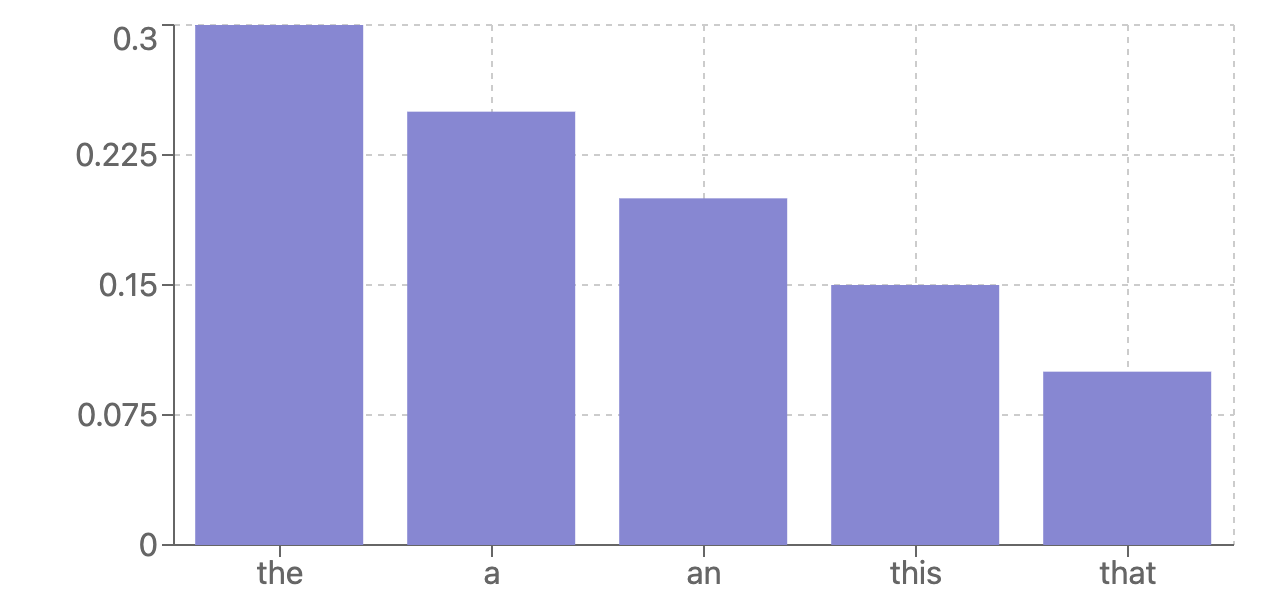
The model has no clear favorite, but it is more certain in some outputs than others. This is a difficult place to be in. One way to think about is that any of the top options may be solid choices (e.g. they are synonyms to each other), and so we should just choose one at random (aka a higher temperature).
We could also branch, or insert reflection tokens like we have done in previous options.
Branching vs Thinking Tokens
Branching predictions involves following a few logits to see what other tokens they lead to. This is often called MCTS (Monte Carlo Tree Search) and is a method that has been often tried in LLMs to middling success.
A way to think about this is that branching requires using inference compute in a way where the branches cannot benefit from each others compute. One of the nice parts of transformers is that every bit of compute used informs the rest of it via attention.
Thinking tokens are a way of achieving more compute in an uncertain state without sacrificing some of that compute to explore a branch that you might kill.
In this case however, we can be smarter about when we branch, e.g. when we see high varentropy, and avoid letting the branch diverge too much.
Attention Entropy
It’s worth noting that there are other measures of entropy that we might take into account. Entropix uses them slightly to figure out how to modify temperature, but they might be other tools.
Attention Entropy - How much are your attention heads tend to follow specific tokens, vs pay attention to a large number of tokens in the context.
Attention Agreement - How much your attention heads are paying attention to the same tokens as each other, vs different ones.
If your heads have low entropy and high agreement, that can be another signal for you to be confident sampling the highest probability. Low agreement might indicate that different heads are contributing to different predictions, and it might be worth branching.
Does this matter?
The insights in Entropix feel in many ways fairly easy to understand, and not entirely novel, which has been surprising to many.
Evals and benchmarks are still to come, but early results seem to indicate that this could be a promising direction for open source hackers to improve reasoning.